scilabによるプロット:ベクトル場とKdV方程式
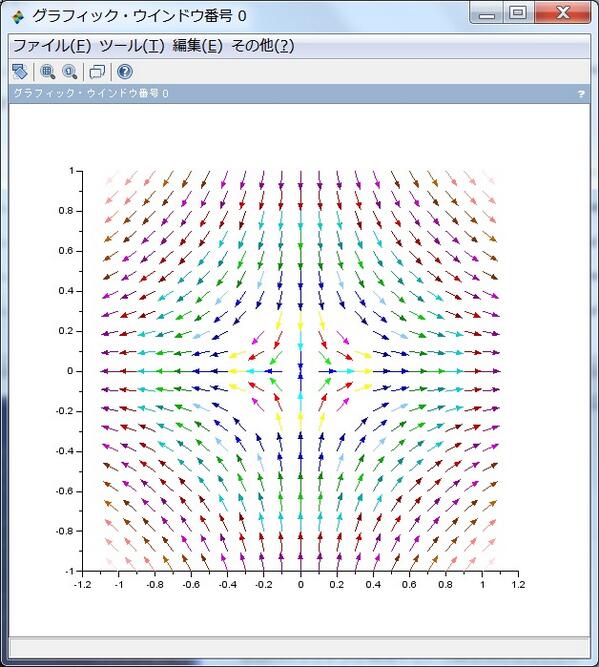
複素函数 f(z) を実数値函数u, vでf(z) =u-ivと表示しておいて、ベクトル場(u,v)を複素平面にプロット。ベクトルの長さは色で表示。流れは面積保存で正則な点では渦なし。添付の画像は f(z)=zpic.twitter.com/ZOu03SBYy2
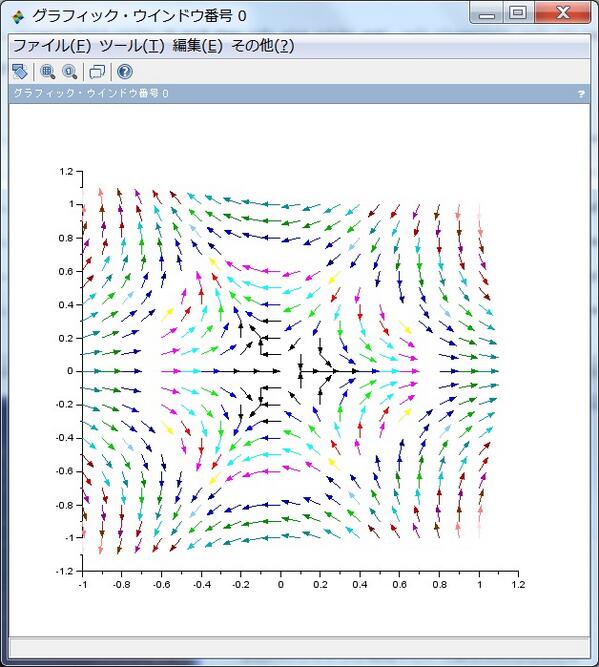
続き。電卓代わりにいつも使っているのがscilabです。添付の図はscilabのchamp1函数によるプロット。添付の画像は f(z)=z^2 です。pic.twitter.com/H0QIGRfCbc
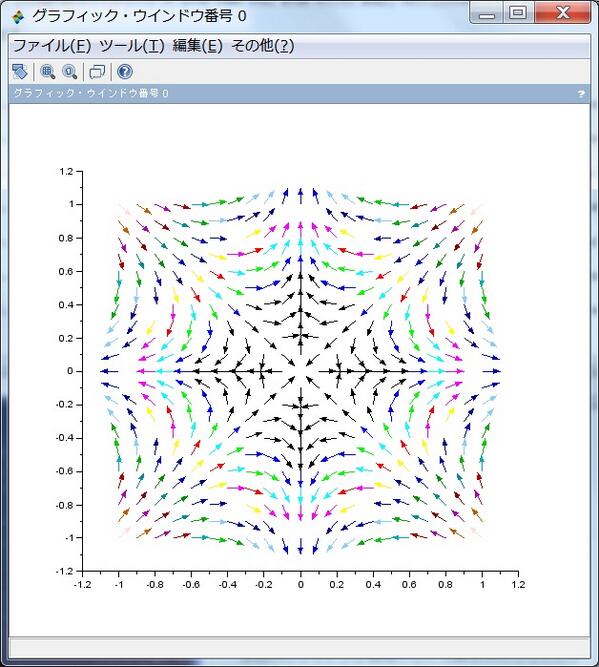
続き。champ1はベクトルの長さを色で表示、長さの通りにベクトルを表示させたい場合はchampを使う。添付の画像は f(z)=z^3 です。体積(面積)保存で渦なしの流れ。pic.twitter.com/NlSBXoH8hx
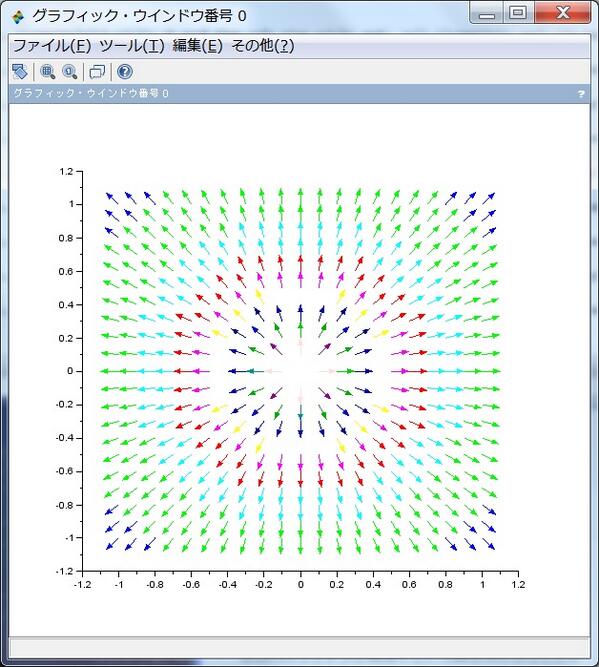
続き。xとyを-1から1まで0.1刻みで動かす。z=x+iyとおいて、f(z)の(実部)と-(虚部)を成分とするベクトルをプロット。ただしベクトルの長さは色で区別。f(z)=1/z です。湧き出しまたは正電荷に見える。pic.twitter.com/t7ZQi7DA5X
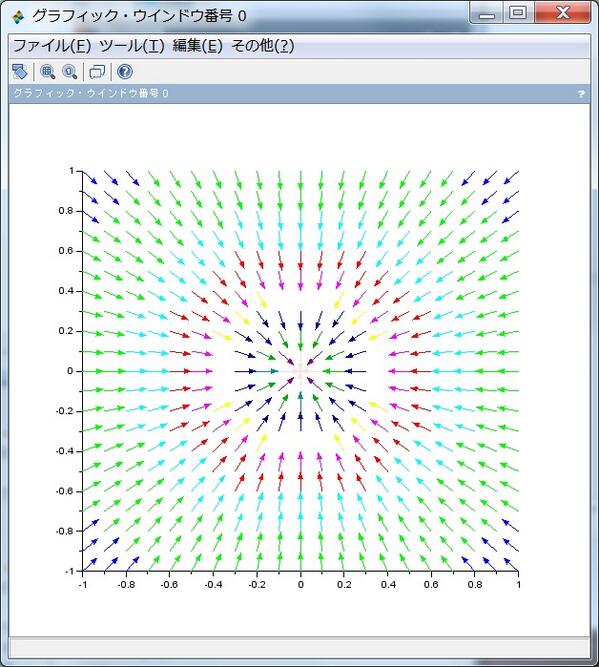
続き。これは f(z)= -1/z です。一つ前の奴の-1倍。これは吸い込み口または負電荷粒子に見える。極でる原点以外では体積保存で渦無しの流れ。原点の極に流体または電気力線が吸い込まれている。pic.twitter.com/hlfY3ZgW9J
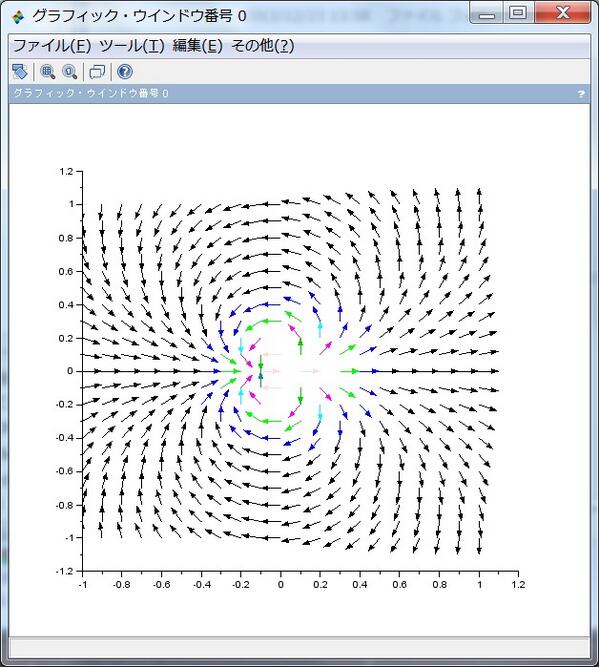
続き。ベクトルの長さを色で表示しているところがちょっと分かり難い。極(特異点)以外では体積保存で渦無しの流れ。f(z)=1/z^2 です。これは正電荷粒子と負電荷粒子がくっついている様子になる。pic.twitter.com/ADpkvHT8i1
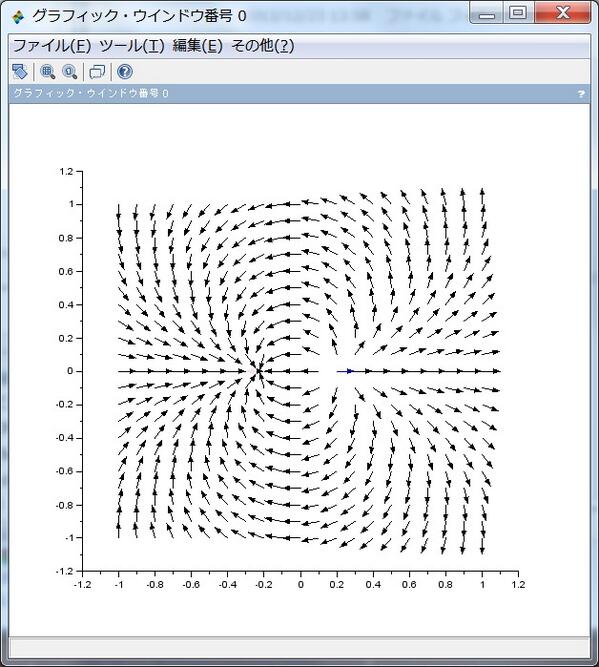
続き。f(z)=1/(z-0.2) - 1/(z+0.2) は正電荷粒子がz=0.2に負電荷粒子がz=-0.2にある様子。1/z^2の様子に近い。pic.twitter.com/uYylpUO9uj
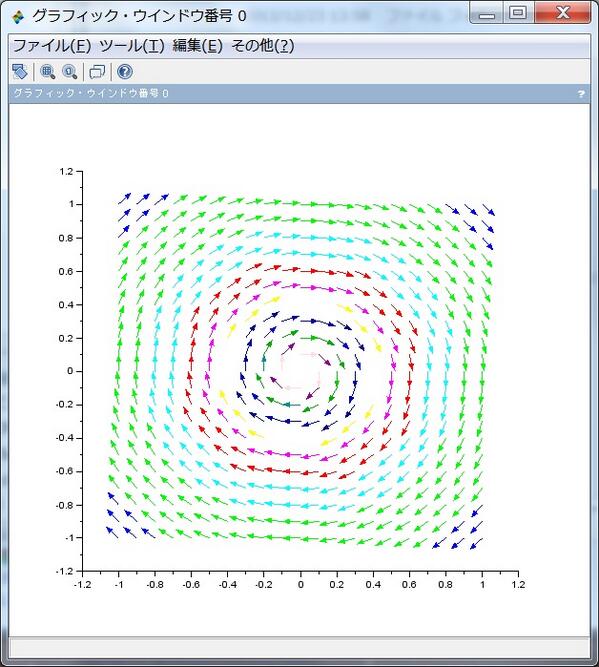
続き。回転する渦を見たければ f(z)=i/z の様子をプロットしてみればよい。ベクトルの長さを色で表示しているのでわかりにくいが、原点では無限大の速さで回転している。これも原点以外では体積(面積)保存で渦無しの流れになっている。pic.twitter.com/BqNA8qP9JT
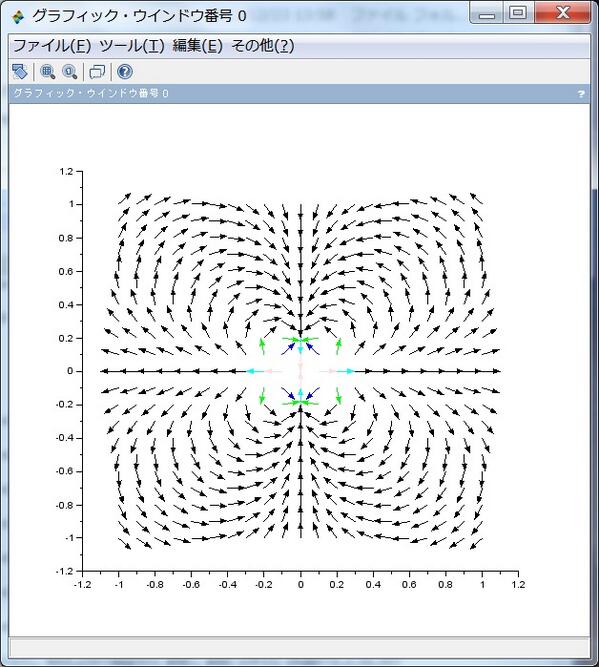
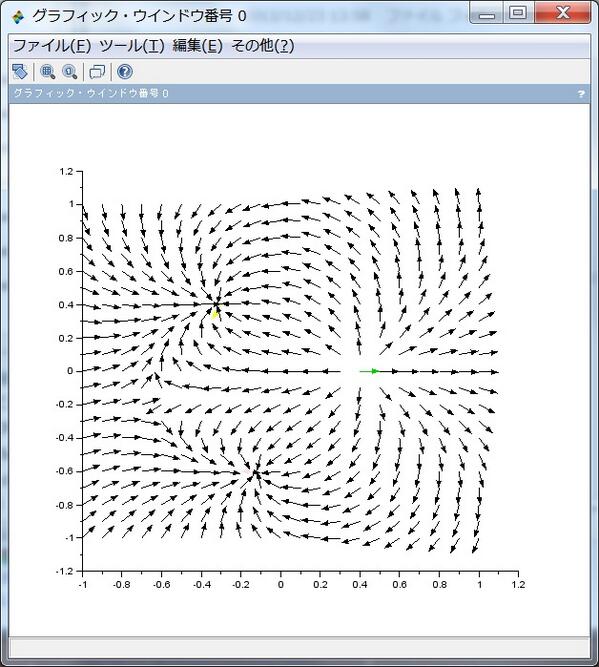
続き。+2の電荷を持つ粒子が一つと-1の電荷を持つ粒子が二つ近くにある様子。これは f(z) = 2/(z-.4)-1/(z+.1+.6i)-1/(z+.3-.4i) です。pic.twitter.com/diBHcAmH8G
続き。複素函数 f(z) を実数値函数u, vでf(z) =u-ivと表示し、ベクトル場(u,v)を複素平面にプロットした。描かれる流れの図が体積(面積)保存かつ渦無しになることとf(z)が正則函数になることは数学的に同値。正則函数は体積保存で渦無しの流れと同じ。
続き。以上では簡単な複素函数の流れのみをプロットしてみた。もっと複雑な有理型函数であっても、零点と極の情報さえ得られれば、その近所の流れを全体で適当に繋げれば全体の流れの図が得られる。ただし、体積保存と渦無しという性質に注意する。
続き。よくある質問【f(z)=u-ivとしていますが、どうしてすなおにf(z) =u+ivとしないのですか?】への回答。虚部を-1倍しているのはコーシー・リーマンの方程式と体積(面積)保存で渦無しという条件が同値になるようにするためです。実際に流れをプロットすればわかる。
続き。scilabの使い方。(1)scilabを使えるようにする。無料。ググれ。(2)scilabにclear; x=[-1:.1:1]; y=[-1:.1:1]; [xr xc]=size(x); [yr yc]=size(y);と入力。xとyは-1から1まで.1刻み。
続きfor i=1:xc, for j=1:yc, z=complex(x(i),y(j)); if z==0 then v=0; else v=1/z; end;, vx(i,j)=real(v);, vy(i,j)=-imag(v); end;, end;と入力
続きclf(); champ1(x,y,vx,vy)でベクトルの長さが色で表示されたベクトル場が表示される。色を使わない場合にはchampを使う。たったこれだけです。
続き。scilabに限らず、多くの人が使っているソフトの使い方はググればわかる。

以上のscilabで複素函数のベクトル場をプロットする話のまとめ読みはhttp://twilog.org/genkuroki/date-140301/allasc …でできます。添付の画像は f(z)=z です。pic.twitter.com/ZOu03SBYy2
scilabでの等高線の描き方https://help.scilab.org/docs/5.4.0/ja_JP/contour2d.html …たとえば先のツイートの入力の続きでcontour2d(x,y,vy,21);とかすればいいのか。最後の21は等高線の本数。
KdV方程式の数値計算をscilabで 以下のコードは本質的に http://www.wikiwaves.org/Numerical_Solution_of_the_KdV … より N = 256; x = linspace(-10,10,N); delta_x = x(2) - (cont) http://tl.gd/n_1s0rtqt
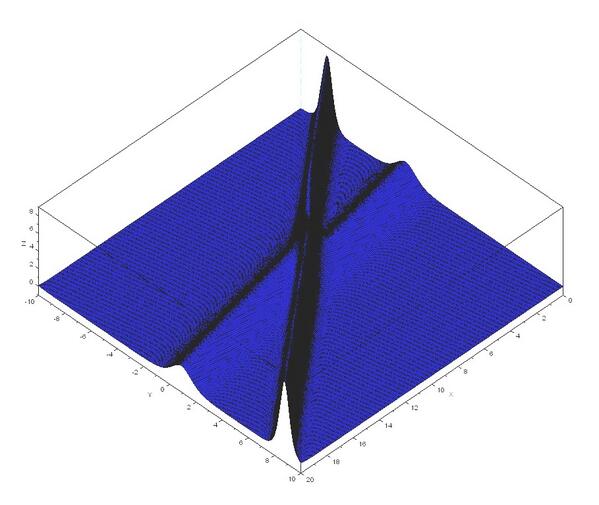
scilabの話 http://togetter.com/li/636897 の続き。KdV方程式の数値計算をscilabでやってみる→ http://www.twitlonger.com/show/n_1s0rtqt 結果は添付画像の通り。所要時間数分間。pic.twitter.com/XYTBc23q7V
scilab話続き。方法はhttp://www.wikiwaves.org/Numerical_Solution_of_the_KdV …より。たったの十数行でKdV方程式を数値的に解ける!もとのコードはmatlabだがほんの少し書き直すだけでscilabでもそのまま使える。
https://twitter.com/genkuroki/status/442318369643954176 … からKdV方程式の数値計算について連ツイしました。scilabを使えば無料でコードはた.. http://togetter.com/li/636897#c1407830 …

投稿し直し。pic.twitter.com/XYTBc23q7V画像はKdV方程式の2ソリトン解の数値計算の結果。実際の初期値は2ソリトン解の厳密な初期値ではない。近似。scilabを使った。KdV方程式のWikipediahttp://ja.wikipedia.org/wiki/KdV��程式 …

pic.twitter.com/XYTBc23q7V添付のグラフを作るためには、(1) scilabを自分のパソコンにインストール(2) scilabを起動(3) http://www.twitlonger.com/show/n_1s0rtqt の後者のコードをコピー&ペーストこれだけ。

pic.twitter.com/XYTBc23q7V数値計算http://www.twitlonger.com/show/n_1s0rtqt で使ったコードはほぼhttp://www.wikiwaves.org/Numerical_Solution_of_the_KdV …のmatlab用のコードのコピー。虚数単位のiを%iに書き変える程度の変更でそのままscilabで使える。

再掲 pic.twitter.com/XYTBc23q7VKdVの数値計算http://twitlonger.com/show/n_1s0rtqt たったの十数行のコードはhttp://www.wikiwaves.org/Numerical_Solution_of_the_KdV …にあるmatlab用コードのコピー。ほんの少しの変更でそのままscilabで使える。

#数楽 再掲 pic.twitter.com/XYTBc23q7V KdVの数値計算http://www.twitlonger.com/show/n_1s0rtqt はほぼ http://www.wikiwaves.org/Numerical_Soluion_of_the_KdV … のmatlabコードのコピー。虚数単位のiを%iに書き変える程度で無料のscilabで使える。



